The first time I encountered the word “meme” was in a Richard Dawkins book prior to the age of the internet. “Meme” meant an original idea that outlived an individual— like a gene. Now it’s come to signify a graphic, often propagandistic in nature, spread on cell phones and often without reflection. Having said that, I must confess to having spread sports and science “memes” in the current, vulgar sense of the word. If you over-microwave a dish of prepared mac and cheese, something which, according to the meme, “real Italians” would never eat, the carbon content of the of the meal becomes apparent. Apply pyrolysis to dead trees, animals or any living form you can think of and the result will be a similar lump of carbon. Life not only depends on water’s remarkable properties but on the sixth element of the periodic table.
Captain Kirk cautiously approaches a life form that is supposedly based on silicon, a highly unlikely scenario given silicon’s chemical properties, which are the same throughout the universe. The bocce ball-like spheres in the background are the creature’s eggs. Image from cbs.com
In the original Star Trek, Episode 26, The Devil in the Dark (1966) there’s an emergency on Janus VI, a seemingly uninhabited planet, rich in metals and rare minerals crucial to Federation operations. There is however a swift-moving, unseen monster roaming the snaky tunnels of Janus’s interior, turning miners into acid-drenched goo. Fifty men have died, and Captain Kirk Mr. Spock and Dr. McCoy) beam down to start the detective work. Spock surmises that silicon-based life is behind the mystery.
As much as I loved Star Trek, a silicon-creature is not an example of good science on TV. Although silicon has the same valence number as carbon and is in the same periodic table family, Si’s chemistry is different enough to make silicon-based life highly improbable. Carbon can make chains(catenate) with atoms of its own kind and makes discrete molecules with oxygen. Silicon does not. Life’s key molecules (proteins, lipids, nucleic acids and carbohydrates) depend on the existence of CO2 and carbon chains and the way the latter can incorporate other atoms, especially hydrogen, oxygen, nitrogen, phosphorus and sulfur.
For the uninitiated, let’s take some time to explain “valence” and “ability to catenate” with what will amount to playing a “fun game”, as many of my students described it. Elements, which have only one kind of atom, characterized by the number of positive particles(protons) in their nuclei, can bond with other atoms of their type and/or with different atoms to form compounds. Each different compound has its own signature, a unique combination of physical properties and chemical behaviour towards other substances. Of course. there are meaningful patterns and similarities based on the type of bonding, but what exactly is a bond?
A bond is an attraction between two atoms, and although there are a variety of bonds the one most important to carbon atoms is one based on sharing, a so-called covalent bond. Imagine you and a partner each having a ball. As you throw your ball towards your partner, he does likewise. You each catch the incoming ball and then throw it back. To keep this going, no one will go too far or too close; you will be bonded to each other. Although each of you contributed a ball, both of you can claim a kind of ownership for the pair of balls. Each covalent chemical bond is similar to that ball-tossing; there are two electrons per bond and the electron pair is shared by two neighboring atoms. But the ball-tossing is not the “fun-game” I was referring to.
If you have two functional hands and a pair of tennis balls, you could in fact bond to a couple of ball-tossing friends, even if each friend has one hand tied up eating an apple. If you were on your back and had great agility, you could use your feet and start off with four different balls and make four bonds. To get the structural arrangement of carbon compounds, to see and understand how it could make chain-like molecules or in other words catenate, we need to know how many “balls” each player starts off with and also how many balls each player is capable of tossing.
We have already mentioned that the balls represent electrons— but not just any electron—they represent valence electrons. Most atoms have “balls in their pockets”; they have non-valence electrons, which do not participate in covalent bonding. The valence electrons which are available for bonding are the ones most exposed to neighboring atoms; they are the ones from the outermost energy level, which we will discuss later. For several of life’s essential elements, we can easily get the number of valence electrons and predict the number of bonds they will make by simply looking at the periodic table.
Figure 1 highlights five of life’s essential elements, hydrogen(H), carbon(C), nitrogen(N), oxygen(O) and chlorine (Cl).
Now we are ready for the game. To get the number of valence electrons for each of these atoms simply start on the left and count across the row, until you get to the element. We get the following:
|
Element
|
# of Valence electrons |
|
H
|
1 |
|
C
|
4 |
| N |
5
|
| O |
6
|
| Cl |
7
|
How do we get the number of bonds or the number of balls that each atom can juggle? The physical rationale for this rule of the game will be explained in the chlorine chapter, but for now, simply subtract the valence number from the number of elements in the row of the element. For example, there are two elements in hydrogen’s row; its valence is 1, so it will make 2 – 1 = 1 bond. There are 8 elements in nitrogen’s row and with a valence of 5, it will make 8 – 5 = 3 bonds. The table can now be extended to the following:
|
Life-essential element
|
# of Valence electrons |
# of bonds |
|
H
|
1 |
1 |
|
C
|
4 |
4 |
|
N
|
5 |
3
|
| O |
6 |
2
|
|
Cl
|
7 |
1
|
Now comes the fun-part. How, as an example, do get the structural (bond arrangement) for carbon dioxide, CO2? Carbon comes into the game with 4 valence-electrons, while each oxygen comes in with 6. Using a dot to represent each valence electron:
Since carbon will make 4 bonds and each oxygen, only two apiece, we can satisfy everyone by having the carbon make 4/2 = 2 bonds with each oxygen.
We can simplify the above dot structure by connecting the bonding electrons and ignoring the non-bonding ones, always keeping in mind that there are only electrons per bond, and we will obtain a “structural formula”.
Here’s a more elegant looking one with a three-dimensional look:
What about an example where carbon catenates? Butyric acid is a fatty acid that can be obtained by breaking down butter fat or some plant oils. Its molecular formula is C4H8O2. If you look up that formula in the Merck Index, a chemical dictionary of sorts, you will notice that there are eight different compounds with that same formula. In other words, you could follow the rules we’ve mentioned but come with 8 different ways of satisfying them. To zero in on the actual structure, you would need additional clues. You need to be told that butyric acid resembles other fatty acids that are used as soaps (more of that in chapter 4), which have a snake-like part in their structure to sink into grease and a CO2H part to attract water. The latter looks like this and characterizes it as an organic or carboxylic acid: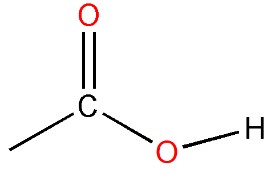
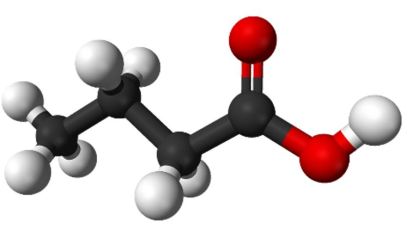
This part uses up one of the 4 carbons in C4H8O2 , one hydrogen and both oxygens, leaving us with 3 other carbons and 7 hydrogens to make up the snake-like part. In a single molecule, the “one-handed” hydrogen can never be sandwiched between two other atoms since it only makes one bond. We can place a carbon at one end of the snake bonding to three hydrogens. To make its fourth bond, carbon can bond to one of its own. The other pair of remaining carbons will do likewise, but since each carbon is sandwiched, each atom only needs a pair of hydrogens. And here we have it, this is the structure of butyric acid:
In 3D the model would look like this, although, in reality, the bonds don’t make a tunnel-like structure.
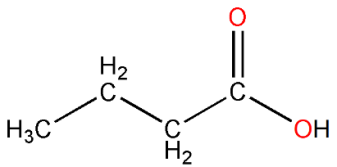
Unfortunately for outsiders, there is a graphic jargon among organic chemists that crops up in books, scientific journals and all over the internet. To save time, even though it mystifies everyone else, the shorthand leaves out the hydrogens that bond to carbon atoms and represent carbons as vertices and endpoints, highlighting only the remaining bonds. As an example, butyric acid’s structure would be drawn like this:
Throughout this book I will not use the above shorthand, but a compromise between the shorthand and the original structure we drew; I will draw butyric acid and other structures using this convention:
Now we can get back to the Star Trek episode and not just to the unlikelihood of silicon-based life but how carbon-chemistry facilitates life. Silicon is the second most common element in the earth’s crust; life does use it but just sparingly in the exoskeletons of certain life organisms. That implies that, given its chemistry, that’s about all it could manage to do with the element. Silicon’s most common oxide is sand, which lets the liquid of life just trickle through itself. The fact that carbon’s most stable oxide, carbon dioxide, exists as a gas means that it can be harvested from the air by the base of the food chain. Equally important, whenever chemical bonds are formed, energy is released, and a great deal of that happens when water and carbon dioxide are created from oxidizing sugars. Why?
To break bonds is an uphill climb. When someone literally climbs a hill, he is fighting against gravity and does work, which is proportional to gravitational acceleration, his mass and the height he climbs. To break a bond, one is working “uphill” and against the electrostatic force between each positive nuclei of the atoms invested in the bond and the electrons they share. Do the reverse, and it’s a downhill ride; and energy will be released. In many reactions, both bond-breaking and bond forming occur. In making a sugar, the energy gained from forming the bonds of glucose does not compensate for the energy required to break the bonds of the necessary ingredients: water and carbon dioxide. It needs an input of solar energy and a sophisticated network to be able to invest it adequately. This implies that there is a fair amount of energy involved in the pair of C=O bonds in CO2 and the pair of OH bonds in H2O. For reasons we shall explain later, this is partly due to oxygen’s pull on the bonding electrons, which is stronger than that of either hydrogen or carbon. But equally important is the ease at which these bonds can form. When we go backwards, and form water and carbon dioxide from glucose, the energy released from the formation of the products more than compensates for what is needed to break down glucose.
But why can’t we have discrete molecules of SiO2 that fly off like carbon dioxide instead of a solid network of silicon and oxygen in a two to one ratio? To answer the question, we will have to probe a little deeper into the periodic table and into bonding.
Why does the periodic table have an odd shape? Why aren’t the elements presented in a nice, rectangular arrangement?
Figure 2. Elements bordered in orange have some of their valence electrons in p orbitals, whereas those shaded in turquoise have them only in the s orbitals. The ones in the middle begin to fill a d orbital from a lower energy level before moving on to the p orbital. Technically, the type of orbitals—- s, p, d and f (beginning in rows with elements 58 and 90) —correspond to quantum number l-values of 0,1,2 and 3 respectively. But why are they designated with the letters s, p, d and f? In the 1880s, while drawing analogies between the spectral lines of alkali metals and sounds, they described the lines as being sharp, principle, diffuse and fundamental. After quantum numbers were assigned to elements in 1926 based on the solutions to Schrodinger’s wave equation, Sommerfeld and Hund borrowed the s,p,d and f letters, and they became commonly used in the 1930s.
When we assigned 4 valence electrons to carbon and 6 to oxygen, we gave the wrong impression that they all resided in the same place—all from the second row which represents the second energy level—whatever that was supposed to mean. Electrons can act as particles but when things are that small, their wave properties are crucial. The consequence of their wave-like nature is that we can never be certain where an electron is at any given time. Carbon’s four electrons in the second energy level are generally further away than the pair from the first. One pair is very likely to be somewhere in a spherical region, called the s orbital. The other pair are in two of three separate dumb-bell shaped orbitals known as p orbitals. All the elements bordered in orange in the periodic table of Figure 2 have some of their valence electrons in p orbitals, whereas those shaded in turquoise have them only in the s orbitals.
Figure 3. The atomic orbitals of carbon. One p orbital is unoccupied. Source: modified version of diagram khanacademy.org
Each p orbital is along one of three axes, x, y and z. (Figure 3) The non-valence electrons of carbon from the first shell are in the 1s orbital. If an atom only has those two electrons, it is either a hydride ion (a negatively charged hydrogen with an extra electron), a neutral helium (He), Li+ or Be+2, (lithium or beryllium which have lost 1 or 2 of their original 3 or 4 electrons, respectively). But unlike the previous set of elements, carbon has four other electrons, two in the 2nd energy level’s s orbital (deep orange sphere in Figure 3) and, since carbon is in the second column of the p block, two valence electrons in two separate p orbitals.
Focusing only on carbon’s valence electrons, they ware arranged like this:(The different arrows represent opposite spin properties.)
If we do the same for oxygen which has 6 valence electrons, we get the following, and if you haven’t anticipated it already, we will have a problem if we imagine combining these orbitals to create CO2. If carbon’s pair of partially filled p orbitals are shared with one oxygen atom’s pair of partially filled p’s, we can imagine their respective lobes overlapping in the 3D view, but then carbon won’t be able to bond to a second oxygen. Yet in reality, it does form a very stable molecule. How does it happen?
Molecules do not necessarily form by keeping the original atomic orbitals of their constituents exactly as they originally were. The whole can be, not the sum of the parts, but a hybrid of at least some the parts.
Imagine an s orbital from carbon’s valence energy level hybridizing with one of the three p orbitals two create two new sp hybrid-orbitals. That would still leave a pair of p orbitals intact, and then the four valence electrons would be distributed among the four orbitals like this:
Meanwhile each oxygen’s orbitals also hybridize but by using two p orbitals and one s orbital to create a trio of sp2 orbitals (The superscript indicates that two p’s were used.) Each oxygen’s new configuration would then look like this:
Looking at them together, we can see how the pair of double bonds form:
Figure 4. Detailed view of bonding in CO2 molecule. Diagram by author.
Each bond is represented by an oval. Notice that the double bonds are not identical. One results from an sp2-sp overlap, while the other is from the overlap of p orbitals. When viewed in 3-D we see why the CO2 molecule is indeed linear. (Figure 4) Finally, we can now answer the question, “Why not SiO2?”
If we imagine substituting silicon with its four valence electrons for carbon in the above, we run into a problem. The outer p orbitals of silicon, unlike carbon’s are not from the same energy level as oxygen’s. This results in a poor overlap. A more stable arrangement is obtained if in bonding with oxygen, silicon hybridizes its orbitals like carbon does when single-bonding to itself or to hydrogen. It forms four sp3 hybrid orbitals and single-bonds to four oxygen atoms. But since oxygen becomes more stable by forming two bonds (this will be explained in detail in chapter 10), each oxygen bonds to another silicon. As a result, instead of getting a discrete molecule and an analogue of CO2, we get a crystal network of Figure 5.
Figure 5. Instead of double bonding to two oxygens, silicon forms single bonds with four oxgens, which in turn each bond to another silicon atom. The preference for this structure over discrete molecules like SiO2 is the reason that silicon-based life is unlikely. Source: Introduction to Inorganic Chemistry (http://creativecommons.org/licenses/by-nc-sa/ 3.0/)
As Dr. McCoy points out in Star Trek, silicon loves to catenate with oxygen to create quartz and similar minerals. But the writers went ahead and created the silicon egg-laying creature anyway.
Figure 6. Hybridization of carbon’s 2nd energy level orbitals to form four sp3 orbitals.
Regarding carbon’s sp3 hybrid orbitals, when and how do they form and why is there a 109.5o angle between the bonds? They form whenever carbon makes four single bonds with itself and/or hydrogen and other atoms. That’s saying a mouthful because at least one carbon makes four single bonds in most of the molecules of life. If we use methane as a simple example, carbon’s three 2p orbitals can hybridize with its 2s orbital to form four sp3 orbitals (Figure 6). Each sp3 orbital can then overlap with the 1s orbital from each of four hydrogen atoms to yield four identical single bonds.
Figure 7. This visualization can be used to easily calculate the tetrahedral angle of 109. 5º. Diagram by the author.
The four bonding pairs of electrons repel each other and in three-dimensional space, the way they can get as far from each other as possible is to form a tetrahedral bond. To understand why the tetrahedral angle is 109.5o, imagine two of the hydrogens being at opposite corners of the face of
a cube closest to you. The other hydrogens are at the opposite diagonal of the cube’s face furthest away from you (Figure 7). If we assign two units to each side of the cube, the carbon atom is at the center of the cube and is thus halfway up the cube, or 1 unit away from the base. One of the identical tetrahedral angles (2q) is part of a triangle (in red) formed by the carbon and the hydrogens at the bottom of the cube. Using simple trigonometry (Figure 8), q can be calculated to be 54.736o, which means that the tetrahedral angle = 2q= 109.5 o.
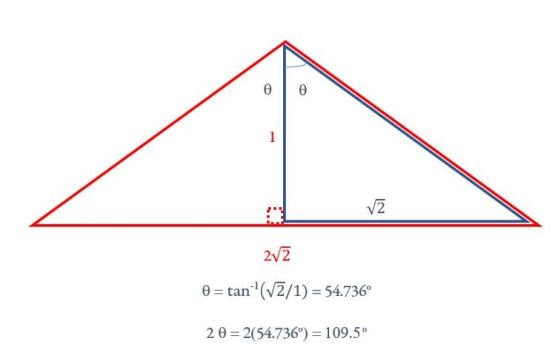
Figure 8
Given carbon’s ability to catenate, can it be found alone on Earth, that is to say, in its elemental state and unbonded to other elements? Forest fires never convert trees to just carbon dioxide and water. There simply is not enough oxygen and heat to do so. The additional products include soot and charcoal, both of which contain elemental carbon. Both soot and charcoal contain very small amounts of one of the most elegantly shaped molecules known to date, buckminsterfullerene.
Imagine starting off with one of the five Platonic solids, an icosahedron(part (1) of Figure 9), which has 20 triangles and 12 vertices. You cut below each vertex, parallel to the pentagon (solids 2 and 3). That creates 12 pentagons and several hexagons. How many?
Figure 9. 1 2 3 4 Getting the shape of buckminsterfullerene from an icosahedron.
For each side of a pentagon there is a hexagon, but it is shared by three other pentagons, So the total number of hexagons = 12 X 5/3 = 20. There are 5 vertices per pentagon, every one of which is also a vertex of a hexagon. In all there are 5 X 12 = 60 vertices. Buckminsterfullerene has a carbon atom at every vertex, so its formula is C60.
Why are there double edges along half of each hexagon? Carbon’s four valence electrons lead to four bonds. Each “double edge” symbolizes a double bond. Each hexagon has three double bonds, each of which is shared with another hexagon, leading to a total of 20 X 3/2 = 30 double bonds. The remaining 3 single bonds per hexagon are not shared with hexagons, so there are a total of 20 X 3 = 60 single bonds in C60.
Figure 10 Graphite’s structure
What if we had no pentagons, and just flat sheets of hexagons with a similar network of alternating double and single bonds? (Figure 10) Then carbon would be forming graphite. Naturally found in ore deposits, graphite is used in pencils and some lubricants. The bonds between the sheets of graphite are intermolecular and not as strong as the bonds resulting from shared electrons. It’s the reason that it’s so easy to break a pencil. But at the right temperature and under the necessary pressure, graphite’s carbon atoms can form nothing but single bonds in a tough tetrahedral structure of carbon atoms, known as diamond.
There is a remarkable similarity between the structures of ice and diamond and an even more remarkable difference. (Figure 11)Each H2O molecule in ice and each carbon atom in diamond make four bonds with their own kind, leading to the same three-dimensional shape.
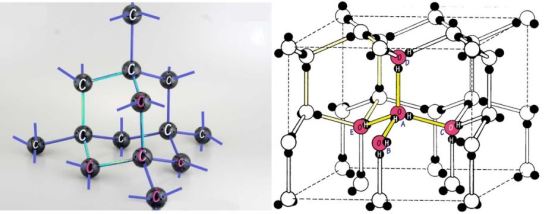
Figure 11. The structures of both diamond and ice form tetrahedral arrangements. Hexagonal arrangements are highlighted in both. But the four covalent bonds made by each central atom in diamond are much stronger than water’s H-bonds.
But diamond is so much harder then ice because shared electrons create covalent bonds between carbon, whereas the hydrogen bonds between water molecules are of an electrostatic nature. Diamond can not only cut through glass and steel, it can also support powerful lasers’ shock waves equivalent to almost a million times our atmospheric pressure. However, ice’s strength, albeit magnitudes weaker than diamond’s, should not be underestimated, as anyone who has had to use a pick to break ice can attest. (Less-known evidence of hydrogen bond tenacity comes from the practical joke of leaving a wet newspaper on a windshield in sub-zero temperatures).
I don’t think da Vinci would be too impressed with any of the above! He may very well have told me that I would be better off spending time drawing, painting or inventing something, the pastimes that he cherished the most.
Sciences in the Mural of Life 