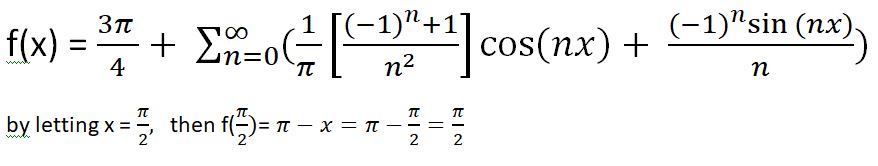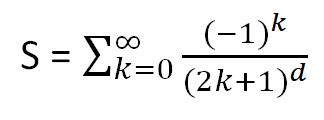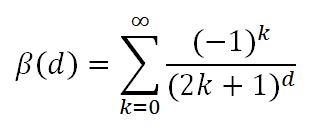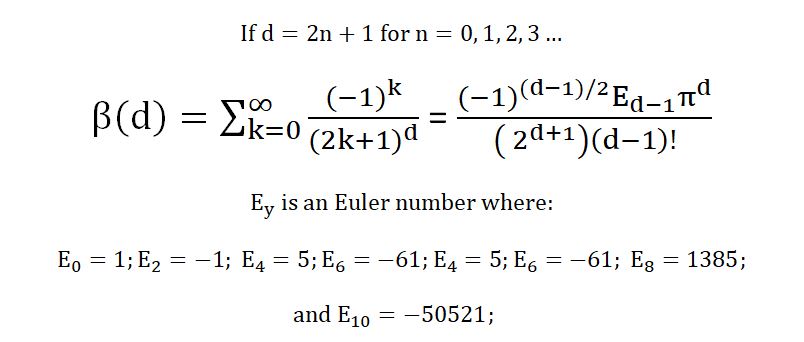Human minds are a funny thing. Take mine for instance. When I first heard of special relativity in a college physics course, I found it refreshing, but unfortunately not powerful enough to encourage me to pursue it beyond our subject’s superficial introduction. Years later, I went back to the derivation of the gamma factor and that of E = mc2, and I found it as inspiring as the Pink Floyd’s Meddles album that played in my head while I sat in physics class.
Similarly, a friend of mine who developed mathematical models to test new designs of airplanes wondered why I had aborted my math education while majoring in chemistry. In my old age I have gone back to learning math, almost on a daily basis (albeit at a snail’s pace) while that same retired friend is more interested in pursuing his passion for music, probably because math reminds him of work.
Given that I will probably bore him again with another math story; given that my wife will refuse to listen to it outright, while my daughter would only take a polite interest in it while killing the minutes during her walk to the lab— I will tell you about it instead.
Consider the following infinite sum, S, of the form
In the denominator consecutive odd numbers are raised to the same power,d . As we alternately add and subtract more and more terms, the series converges to a fixed number. For example, for the power of 1, ( d = 1):
the first four terms give a result of 0.8349….. If you use a total of 8 terms, we get 0.81309…. Eighty terms produces 0.78848… When we add and subtract 800 terms, the first two decimals don’t change as the series yields 0.78571… The third decimal becomes steady as we move to 1500 decimals. With 15000 terms, we get 0.78541… which looks like π/4 = 0.78540. If we use different odd powers for the sums, an interesting pattern emerges:

Notice that the power of π is always equal to d. Less obvious is that the denominator equals 2d+1 times (d-1)! For example, for d = 1, the denominator equals (21+1) (1-1)! = 4(1) = 4. For d = 5, it equals (25+1) (5-1)! = 64(4*3*2*1) = 1536, and so on.
There is a more succinct way of expressing the sum by using the symbol sigma:

For any whole number d value, odd or even, there is a Dirichlet beta function that’s defined as
So according to our table,
To express our pattern for odd powers of d, then we define x = 2n+ 1 , which means that n= (d-1)/2.
For those familiar with calculus there’s another beautiful relationship between the Dirichlet beta function and an integral. It’s :