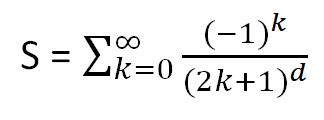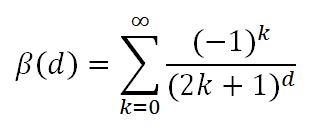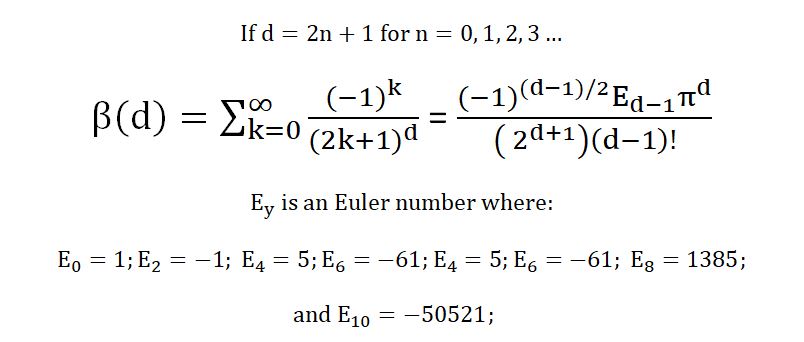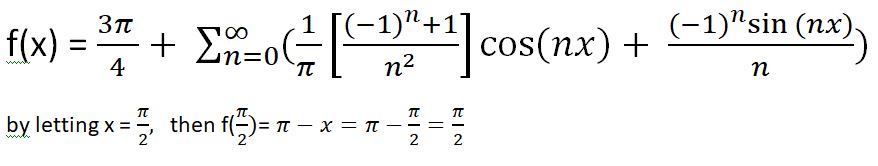The Chemistry of Inks: Old and New

                When we write the old-fashioned way, with ink on paper, we rarely think of the pen’s ingredients. For hundreds of years gall ink was used to produce documents such as Shakespeare’s Will and the U.S. Declaration of Independence. The drafts of the latter were written on hemp paper, whereas, luckily, parchment made from sheepskin was used for the final copy. Why did it matter?

From Shakespeare’s Will https://shakespearedocumented.folger.edu/resource/document/william-shakespeares-last-will-and-testament-original-copy-including-three

                For starters, let’s discuss what gall ink is. Oak leaves produce tannins to protect themselves from insects and other herbivores. But certain species of small wasps can inject venom and an egg into the base of a leaf bud. A spherical colored ball, known as a gall, then develops around the egg to protect and nourish it. The compounds within the gall include tannic acid. If mature galls, which turn brown, are pulverized and the powder is added to water, it can be boiled and filtered. Centuries ago, someone thought of adding ferrous ion (Fe²⁺) from rust to the concoction and watched it turn blue-black. When gum arabic, a natural gum from the Acacia tree was added, the dark pigment could stick to paper.  An ink was invented.

Galls from parasitic wasps. https://extension.oregonstate.edu/forests/tree-care/do-you-know-what-galls-me-cynipid-wasps

                What caused a chemical change was the formation of a complex between tannic acid and Fe²⁺. Once stuck to the paper, thanks to gum arabic, oxygen from the air snatches an electron from each iron ion to change it to Fe³⁺. This further darkens the ink, but more importantly, it makes it water-insoluble. The problem is that if a cellulose-based paper is used, the Fe³⁺ can in turn act as an electron-thief and degrade the paper. Acids in gall ink unfortunately also help humidity attack cellulose in so-called hydrolysis reactions.   

                Thanks to the late 19^th century discovery of triaryl methane dyes, ballpoint pens do not use gall ink. The 4 most common pigments in modern blue ink are Basic Violet 3 and 4 and Basic Blue 7 and 26.  Basic Violet 3, which is also known as Crystal violet, was used as an antiseptic and fingerprint developer, and it still serves as a good bacterial stain. Basic Violet 4 is similar to 3, except that there are a pair of ethyl(CH₂CH₃-) instead of methyl(CH₃-) groups attached to each nitrogen atom in the molecule. The Basic Blue dyes feature an aromatic ring which shifts the maximum wavelength of absorption causing a reflection of blue instead of violet hues. Their common names are Victoria Blue BO and B, respectively, and they are also used in the blue smoke of fireworks displays. 

The Structure of Basic Violet 3
C₂₅H₃₀ClN₃

                Of course, one needs a solvent to dissolve the colorants, which is why ballpoint cartridges include benzyl alcohol or phenoxyethanol. The latter has germicidal properties, which is why it’s used in many vaccine formulations; benzyl alcohol, whose toxicity is also low, can be obtained either from the petroleum distillate, toluene, or from jasmine’s essential oils. Both solvents are capable of dissolving fatty acids or polymers, which serve as a lubricant , so the ink can roll smoothly around the tiny ball at the tip of the pen.

Two common ink solvents: on the right, benzyl alcohol(C₇H₈O). Right: phenoxyethanol( C₈H₁₀O₂).

The Importance of Booze

                Learning about ethanol, the most common type of alcohol, can be a lot of fun. It may not dissuade the young and old from using it as a social lubricant, but at least knowledge does not lead to hangovers. Moreover, the moderate to heavy absorbance of facts will never be linked to fatal car accidents, cancer or liver disease.

                From an energy perspective, plants face an uphill battle when converting carbon dioxide and water into glucose. Luckily we have sunlight as a continuous source of energy that allows us to create the orderly set of molecules and pathways known as life on Earth. But the conversion to glucose is not a one-shot deal. There are many in-between steps, with intermediate molecules formed. In reverse, when we see molecules “roll down” from the top of the energy-hill, so to speak, the same truth applies. We can set fire to glucose to release the energy that plants invested in it, but organisms use a pathway to do it far more gradually and peacefully. Oxygen does it most efficiently, but when oxygen was not available, another means evolved: fermentation. Instead of converting an in-between-product called pyruvate to carbon dioxide and water, they turned pyruvate into carbon dioxide and acetaldehyde, with the latter being converted into something less toxic: alcohol.  

                Even now on Earth, when food is available but oxygen is not, yeast and other microorganisms continue to perform the same kind of chemistry. Very ripe bananas, cantaloupes —in fact almost 80% of fruits in Costa Rican tropical forests—contain small amounts of alcohol, compliments of wild yeasts that ferment fruit sugars.  Some lemurs and monkeys have preferences for fruits that are naturally spiked, but only to a degree. Egyptian fruit bats, who help disperse seeds, prefer fruits with 0.1 to 0.7% ethanol over those with concentration greater than or equal to 1%.  Like pilots, they don’t fly as well while under the influence of alcohol.

Egyptian Fruit Bat prefer fruits with low concentrations of alcohol Source: https://www.dudleyzoo.org.uk/animal/bat-egyptian-fruit-bat/

                With alcohol naturally available, it is no wonder that our ancestors learned to make alcoholic beverages such as wine and beer. Nowadays, thanks to chemical catalysts, we can make alcohol from ethylene or even from discarded sugar cane waste. BASF has made use of alumina catalysts and sodium hydroxide, the compound in oven cleaners, to perform the reverse the reaction and consequently convert alcohol into ethylene into a grade that’s pure enough to make the most recyclable type of plastic, polyethylene.

                What else makes ethanol practical? Hand sanitizers contain ethanol, which kills fungi, not bacterial spores but at least kill bacteria cells before they can make more spores. Equally important is the fact that ethanol can dissolve substances that won’t mix with water. We use old booze to clean our whiteboards. Commercially, it’s used as a solvent in paints, some deodorants and in most perfumes. Even more fascinating is the fact that you can create beautiful smells by reacting alcohol with a class of compounds that vinegar belongs to known as carboxylic acids.  One such acid is butyric acid, which smells of rancid butter and is also a minor component of armpit smell. But when “cooked” with ethanol in the presence of a mineral acid, it will convert to ethyl butyrate, which smells like pineapple. In fact ethyl butyrate is an example of a perfectly harmless artificial flavor that can be added to orange juice or candies. In the muck that’s used to make Jamaican rum, bacteria produce a variety of carboxylic acids including butyric acid. And surely enough butyric acid reacts with ethanol from the rum to contribute to the fruity flavor that helps give Jamaican rum its distinctive aroma and taste. 

Ethyl butyrate, a sweet-smelling ester made form ethanol and stinky butyric acid

                Elsewhere in the natural world, we find nearly a hundred different esters produced from either ethanol or other alcohols. After all, an alcohol, chemically-speaking, is a molecule with an OH group attached to hydrocarbon chain, one that could vary in length or shape. For instance, different apple-varieties have varying amounts of alcohol-types. A Golden Delicious will have 10 times more ethanol than a Fuji apple but far less 2-methyl-1-butanol. Not surprisingly the Golden Delicious will have more ethyl acetate but less of the smell from butyl butanate.

                Learning about alcohol’s chemistry is not only in good taste, but it helps us understand why good things can taste and smell so different.    

Funny Minds and the Dirichlet Beta Function

Human minds are a funny thing. Take mine for instance. When I first heard of special relativity in a college physics course, I found it refreshing, but unfortunately not powerful enough to encourage me to pursue it beyond our subject’s superficial introduction. Years later, I went back to the derivation of the gamma factor and that of E = mc², and I found it as inspiring as the Pink Floyd’s Meddles album that played in my head while I sat in physics class.

Similarly, a friend of mine who developed mathematical models to test new designs of airplanes wondered why I had aborted my math education while majoring in chemistry. In my old age I have gone back to learning math, almost on a daily basis (albeit at a snail’s pace) while that same retired friend is more interested in pursuing his passion for music, probably because math reminds him of work.

Given that I will probably bore him again with another math story; given that my wife will refuse to listen to it outright, while my daughter would only take a polite interest in it while killing the minutes during her walk to the lab— I will tell you about it instead. 

Consider the following infinite sum, S, of the form

In the denominator consecutive odd numbers are raised to the same power,d . As we alternately add and subtract more and more terms, the series converges to a fixed number. For example, for the power of 1, ( d = 1):

the first four terms give a result of 0.8349….. If you use a total of 8 terms, we get 0.81309…. Eighty terms produces 0.78848… When we add and subtract 800 terms, the first two decimals don’t change as the series yields 0.78571… The third decimal becomes steady as we move to 1500 decimals. With 15000 terms, we get 0.78541… which looks like π/4 = 0.78540. If we use different odd powers for the sums, an interesting pattern emerges:

Notice that the power of π is always equal to d. Less obvious is that the denominator equals 2^d+1 times (d-1)! For example, for d = 1, the denominator equals (2¹⁺¹) (1-1)! = 4(1) = 4. For d = 5, it equals (2⁵⁺¹) (5-1)! = 64(4*3*2*1) = 1536, and so on.

There is a more succinct way of expressing the sum by using the symbol sigma:

For any whole number d value, odd or even, there is a Dirichlet beta function that’s defined as

So according to our table,

To express our pattern for odd powers of d, then we define x = 2n+ 1 , which means that n= (d-1)/2.

For those familiar with calculus there’s another beautiful relationship between the Dirichlet beta function and an integral. It’s :